Interview with Juan Maldacena

Juan Maldacena is one of the most influential theoretical physicists in the world. His work focuses on quantum gravity, string theory and quantum field theory and it involves different problems such as quark confinement and black holes. Back in 1997, he proposed the famous anti-de Sitter/conformal field theory correspondence, which is also known as the Maldacena duality of gauge/gravity duality. This theory has contributed in the clarification of various aspects of black hole physics, while it has also provided some new tools for tackling complicated problems in strongly interacting quantum field theories.
Following his studies at the University of Buenos Aires and the Instituto Balseiro in Argentina from 1986 to 1991, Maldacena moved to Princeton, where he completed his PhD in 1996. After a postdoc at Rutgers University, he moved to Harvard, where he became a Professor of Physics. Since 2001 he serves as a faculty memberat the Institute of Advanced Studies in Princeton.
We met Juan Maldacena at CERN, during a workshop organized by the TH division and discussed the holographic principle, the motivation behind his work as well as the most recent developments in quantum field theory.
How are black holes described today and what the problems that are we facing?
J.M. There are many aspects to black holes. Let me start by distinguishing the classical from the quantum aspects of black holes. Today, classical black holes are well understood. There are many astrophysical questions that astrophysicists try to answer by observing them. These are aspects for which we have a powerful set of theoretical tools in our hands and a rather good understanding.
The quantum mechanical description of black holes is less understood. One of the most puzzling effects is the presence of Hawking radiation, the thermal, radiation which is emitted by black holes. This effect is not important for astrophysical black holes, since the radiation is too weak to be detected. However, it plays a significant role in the case of very small black holes. It poses one of the biggest problems of how quantum mechanics and quantum gravity can coexist in a consistent theory.
The presence of radiation seems to imply that black holes are losing information. A black hole in empty space would gradually lose its mass due to this radiation. To first approximation, this radiation seems to be unrelated to what fell into the black hole. However, this contradicts the laws of quantum mechanics, since according to QM the emitted radiation should know about the objects that fell into the black hole. In principle, we should be able to calculate what comes out from the black hole so that Hawking’s result emerges from an approximation.
Coming back to your question, on the one hand we know that strong gravitational effects lead to the formation of black-hole horizon; beyond which we have no access, we are not able to see what exists in the interior of this horizon. On the other hand, quantum-mechanical calculations predicted that black holes should emit a thermal radiation that, in principle, should carry information about the matter that formed the black hole. This information appears to reside in the interior. The fact that according to quantum mechanics we need the information and that according to gravity we cannot have it because it is behind the horizon is called the “information paradox”.
Do we have an answer to this problem? What evidence guide our research?
J.M. Today we think that black-holes do not lose information. Instead, that information is preserved and comes out without violating the laws of quantum mechanics.
When we try to describe quantum-mechanical black holes we would like to have two features. First, we want to have a smooth horizon, as dictated by the equivalence principle. We also expect Hawking radiation to carry the information about the black hole.
Gauge gravity duality is one of the approaches that we adopt in order to tackle this problem. It postulates the equivalence between certain quantum field theories and certain space-times. On the one hand you have a quantum field theory on a d-dimensional spacetime and on the other hand a gravity theory on a d+1 dimensional spacetime with an asymptotic d-dimensional boundary. This is a “holographic” approach, since you describe a d+1 dimensional gravity theory in terms of a lower dimensional system.
The simplest case of this duality is that of the AdS/CFT involving an anti-de-Sitter space and conformal field theories. The AdS/CFT relation postulates that all the physics in an asymptotically anti-de-Sitter spacetime can be described by a local quantum field theory that lives on the boundary. In this space-time, black holes correspond to thermal configurations in the particle quantum-mechanical system (i.e. the gauge theory). These thermal configurations obey the ordinary rules of quantum mechanics. If this duality is correct, and we consider black-holes in anti-de-Sitter space, then information is preserved. Hence the laws of quantum mechanics are not violated.
This is so far, more or less, what we understand today. What we still don’t understand is how the ordinary geometric description of black-holes can be recovered. For example why an observer that is falling in a black hole doesn’t observe anything strange; whydoesnt't he feel anything as he crosses the horizon.
Generally, I think that one of the biggest problems is that we don’t understand all the aspects of black holes from the same description at the same time. We have this duality between gravity and the exact quantum mechanical description but we can’t recover all the features of a black hole from only one description.
 What are the “advantages” of this description and this boundary can be understood?
What are the “advantages” of this description and this boundary can be understood?
Imagine that you have a black hole (although you can think of any other object) surrounded by a surface that lies very far from the object. Then, we have two ways of describing what is happening inside. One is the traditional way of quantum gravity as an effective theory while the second is to think that you have a high number of particles that are moving on the sphere that is far away. The particle theory that describes particles moving in the boundary is called the “boundary theory”. Then, any object in the interior can be described as an excitation in this theory.
The two descriptions are equivalent. You can describe everything from the point of view of the boundary or from the point of view of an internal observer. Depending on what you are trying to describe you might prefer to describe it from the interior or from the boundary but in principle both descriptions are equivalent. In practice, there are some properties we can only compute from the boundary or only from the bulk point of view.
However by introducing this boundary theory we translate the problem of describing black holes from the outside to the problem of understanding certain thermal configurations in the boundary theory. There are two advantages in this approach. First, we know that normal particle theories preserve information, hence black holes should also preserve information. In addition, in some cases, it is possible to do concrete computations in the boundary theory which explain some of the quantum aspects of black holes such as their entropy, quasi-normal frequency spectrum, etc.
Is this space time somehow related to the one that we observe in our universe?
In this duality the boundary lies on a spatial direction. At this boundary the gravitational potential (or redshift factor) becomes very large. This effectively pushes bulk excitations away from the boundary. This boundary is where the quantum field theory lies. These spacetimes have negative curvature.
Our space time, the one we live in, has a slightly positive curvature. If the current accelerated expansion goes on for ever, then it would have a boundary in the far future. Our spacetime is closer to de-Sitter than to anti-de-Sitter. In fact, in the early inflationary universe there was also a period of accelerated expansion. We can think of the end of inflation as a kind of boundary. We are sitting in the future of the early inflationary universe and we observe these cosmological fluctuations in the CMB. These fluctuations can be computed by solving equations of perturbative quantum gravity plus a scalar field in the expanding geometry. These quantum fluctuations are almost scale invariant.
Anti-de-Sitter and de-Sitter have very similar symmetry properties. In fact the (almost) scale invariance of cosmological fluctuations is very closely related to the scale invariance that is present in Anti-de-Sitter space. More precisely, we can imagine a generalization of AdS/CFT to a de-Sitter/CFT. This conformal field theory would exist in the future and would allow us to compute cosmological fluctuations by performing a computation in a nearly scale invariant Euclidean field theory. This Euclidean field theory would be similar to the ones used in statistical mechanics to describe systems near a second order phase transition.
This would be a generalization of the CFT where the inflation could be replaced by a three dimensional system and fluctuations could be calculated by using statistical mechanics. Of course this is only a possibility and I am not sure whether it will be realized in the future. Inflation allows calculating the CMB fluctuations in great detail and the holographic picture is not needed in order to get higher accuracy. However, following this holographic description we might shed more light on the initial singularity.
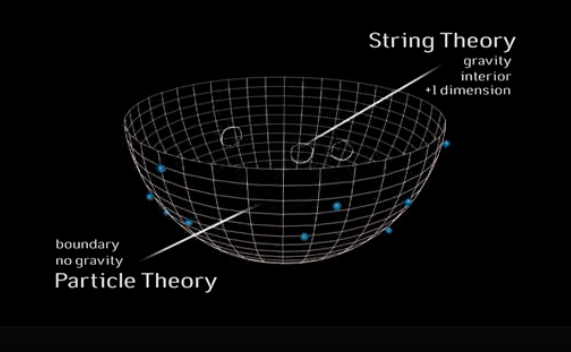
The AdS/CFT duality relates a theory on the boundary of a region to a theory with gravity in the interior. The AdS/CFT duality is a concrete example of holography, which suggests that all the information about the interior of some region is actually contained on the boundary.
Is your research mainly driven by mathematics? If yes, to what extent?
J.M. The research on quantum aspects of black holes is driven by fundamental physics questions. The questions are of a theoretical nature. Since the goal is to get a mathematically consistent picture, mathematical considerations are an important tool. Of course, one is trying to find a description that would be consistent with the laws of physics that are known today.
This problem of trying to reconcile general relativity and quantum mechanics is purely theoretical, for the moment, and can’t be experimentally tested easily. However, it addresses a basic problem of our understanding of nature and it is possible that once it is better understood we will be able to experiment.
These holographic ideas have also been used as toy models in nuclear physics and condensed matter theory. They might be useful as theoretical tools to understand ordinary systems of interacting particles. Or maybe the information will flow the other way. For example, the current theory for electroweak symmetry breaking was inspired by the theory of superconductivity.
We currently have very strong theoretical constraints so it might be possible to come up with a correct theory. Mathematical consistency is a very useful tool that helps us find our way in a field in which is not easy to perform and experiment.
We are exploring properties of string theory as a theory of quantum gravity. There are many dualities and relations between these theories. These dualities point to a connection between quantum field theories, quantum gravity and string theory. There is a kind of unity in theoretical physics. I think that these dualities prove extremely useful in understanding aspects of quantum field theory and quantum gravity. The quantum gravity theorist can use the field theory to understand properties of black holes. The condensed matter theorist can consider the same duality and use the black hole to understand properties of the strongly interacting system of particles.
Since you referred to the importance that this research into black holes poses for our understanding of strong interacting theories I would like to discuss the relation between these dualities and the study of the QGP.
J.M. Indeed, recently there have been interesting studies on the properties of strong interacting field theories from the classical properties of the black holes. The duality postulates that the Quark Gluon Plasma in the boundary theory, in the quantum field theory, is equivalent to a black hole in the bulk theory. By studying the properties of black holes we can learn a lot about the Quark Gluon Plasma.
These quantum field theories are not exactly identical to the theory of quantum chromodynamics. However, it is similar enough, therefore the experienced theorist can extract useful lessons for QCD.
For example, both theories contain gluons. Both theories contain strings; think of the QCD string that joins a quark and anti-quark. In the particular QCD-like theory, where the duality holds, the relation between gluons and strings can be understood in exquisite detail. Gluons form color neutral chains which become strings.
One example where the use of the gauge gravity duality was important is the following. The duality relates the hydrodynamics of the strongly interacting gluon plasma to the behavior of small perturbations of a black hole. When this relation was studied in detail it was found that the small fluctuations of black holes could not be described by the known laws of hydrodynamics. It turned out that there was a term missing from the equations for hydrodynamics. A term that arises when the theory has global symmetries that have anomalies. This new term was discovered using the gauge/gravity duality but it is present for any theory with such anomalies, including the ordinary quark gluon plasma.

A new state of matter, QGP is formed during lead-ions collisions. Above: event display from a lead ion collision recorded by ALICE at LHC.
Should this theory be understood as a mathematical toy or could it point to something that really exists?
J.M. We think that it teaches us important lessons for the quantum mechanics of spacetime. There are also interesting lessons to be learned for quantum field theories, for the emergence of strings from Yang-Mills theories, etc.
What are the cosmological implications of this holographic description?
J.M. There have been some efforts to apply these ideas to cosmology. There are some ideas about how these models that are based on a negatively curved spacetime can be applied in a positive curved universe. One of these ideas is the de-Sitter/CFT correspondence, for which we have one example involving a higher spin theory of gravity.
An important lesson of the AdS/CFT relation is that spacetime is emergent. One of the dimensions of space is not present in the boundary description. Maybe for cosmology we will have a similar situation but time will be emergent.
Does this picture of a holographic universe fits with the Standard Model?
J.M. What is truly interesting is the fact that it seems to fit the SM in two different ways. First, you may think of QCD on its own and a universe that describes QCD. It is a universe that has five-dimensions and is highly curved. In that picture protons and hadrons localize the fifth dimension and excitations of these particles might move in the fifth dimension. We do not know a precise way to realize this relation, but it is quite likely to exist.
Secondly, we might have a description of our universe in terms of a theory living in the far future, in the spirit of dS/CFT. This is something we understand less, even in principle.
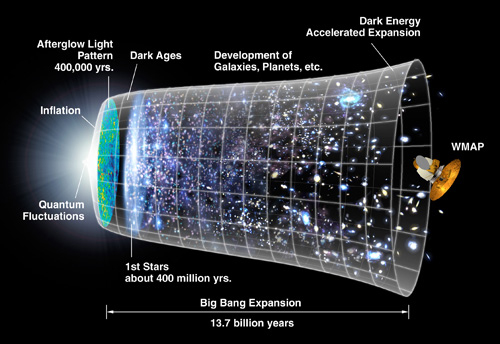
The success of our standard model of cosmology in explaining phenomena observed in the universe today gives us confidence to extrapolate back in time. Was there really an initial singularity, in which all the energy in the universe today was packed into a single point? How could the singularity itself have appeared? These remain open questions, at the forefront of modern gravitational research.
Do you think that this holographic universe might be part of a bigger holographic universe? Could we establish holographic relations within a multiverse?
J.M. The universes for which a dual quantum field theory is expected are distinguished by their asymptotic boundary conditions. For each type of asymptotic boundary condition there is a separate quantum field theory.
When people talk about the multiverse they describe a picture in which all these universes can co-exist in some way, at least as possibilities in a wave function. In that case gauge gravity dualities would be one aspect of this multiverse. We don’t know whether there will be a type of holographic correspondence that could describe the whole multiverse. However, some proposals in this direction have been made.
Are we living in a revolutionary time for physics?
We live in an exciting time. We have understood the properties of primordial cosmological fluctuations, we are experimentally testing the mechanism of electroweak symmetry breaking, we are constraining the properties of dark matter. In the theoretical front, we are uncovering interesting properties of quantum field theories. We have surprisingly new emergent behavior. We are understanding aspects of quantum gravity.
Einstein saw that Newton’s theory and relativity were inconsistent. It took him around 10 years to come up with a consistent solution that would overcome this contradiction. Later, experiments were done that tested his theory with impressive precision. I think that today we try to solve a similar contradiction and, although we don’t have experiments to guide us, we hope that we will find a solution that will be the right theory describing nature. Remarkable progress has been made in the last 30 years but there is still a lot of work to do.
Further Readings:
Black Holes, Strings and Quantum Gravity (2000) (PDF) (HTML) Video Archive
Into the Fifth Dimension (Nature, Vol. 423, June 12, 2003) (PDF)
The Illusion of Gravity (Scientific American, November 2005) (PDF)
You can also visit Juan Maldacena's home page at the Institute of Advanced Studies:
Image Credit: Juan Maldacena photographed by Wim Klerkz in his office at the Institute for Advanced Studies. (Image @ Wim Klerkx, 2002) .
