Q&A: Krishna Rajagopal
An Interview with Krishna Rajagopal, Professor and Associate Head for Education, Massachusetts Institute of Technology Department of Physics.
After growing up in Toronto, Professor Rajagopal did his undergraduate work at Queen's University in Kingston, Canada. He obtained his doctorate at Princeton University in 1993 and then spent three years at Harvard as a Junior Fellow. He then spent one year at Caltech before joining MIT in 1997.
Krishna discusses the opportunities and challenges ahead as we use heavy ion collisions to recreate, and understand, droplets of the matter that filled the microseconds old universe.
He enjoys thinking about QCD in extreme conditions because it requires linking usually disparate strands of physics including condensed matter and cold atom physics, string theory, cosmology and astrophysics, and of course nuclear and particle physics.
In the opening of the QM11 in Annecy you referred to the unique opportunity that the study of QGP offers from a theorists' perspective. Is this still the case?
Quark Matter 2011 was a special conference and it was a particular honour to deliver the opening talk. QM11 was a singular moment in our field since it was the first QM Conference at which experimental results from the LHC were presented.
The study of the Quark Gluon Plasma presents a great opportunity for nuclear physics. On the one hand, we have intrinsic reasons to be interested in the study of the Quark Gluon Plasma as it derives from the fundamental theory of strong interactions and describes the matter that filled the microseconds-old universe. On the other hand, what makes QGP even more interesting is that it is a strongly coupled liquid and as such is an example of a type of matter that arises in other areas of physics including condensed matter, cold atom and black hole physics. In each instance, understanding these strongly coupled liquids presents great difficulties that are seen as central challenges in their respective areas of physics. These are systems with vastly different natural length scales and with temperatures that vary over 20 orders of magnitude (from nanoKelvin-cold droplets of atoms to TeraKelvin-hot droplets of QGP) but they are all fluids with good hydrodynamic descriptions that cannot be described at all in terms of individual quasiparticles that travel some distance between successive scatterings. Precisely because they cannot be understood simply as groups of individual quasiparticles interacting according to some force laws, we need a fundamentally new picture with which to understand these liquids.

Quark Matter 2011, Annecy, France.
Broadly speaking, there are two ways in which nuclear physics can contribute to the understanding of strongly coupled liquids with no apparent quasiparticle description. First of all, we need to characterize the properties of the QGP, “our” example of such a fluid. Considerable progress has been made over the last year. Consider, for example, how far the experimentalists at RHIC and the LHC have advanced since my opening talk at QM11 in measuring v2, ν3, and up to ν6 and thus characterizing how the droplets of QGP flow. We saw at QM12 in Washington that the multifaceted theoretical effort that is needed in order to turn this magnificent flood of precise data into sharper constraints on the initial conditions in heavy ion collisions and on the properties of the QGP that is produced in these collisions is now well underway.
The second broad opportunity for nuclear physics is related to the fact that we have a chance to study the properties of QGP at very short distance scales where QCD is asymptotically free and quarks and gluons are weakly interacting. This means that by using sufficiently powerful “microscopes” we should be able to study how the strongly coupled liquid QGP emerges from weakly coupled short distance physics. The fact that we already know that “our” strongly coupled fluid is made of weakly coupled constituents at short distance scales, interacting according to well-understood forces, gives us a huge advantage over physicists studying the strongly coupled fluids that emerge in other areas of physics. In our field, hard probes give us a chance to access short distance scales experimentally. I am thinking of jet quenching, Y's , J/ψ, heavy quarks, direct photons and combinations of these like photons back-to-back with jets. These observables can provide us with different kinds of microscopes trained on the QGP. This great opportunity is still ahead of us. From a theoretical point of view we need to think about how best to use these observables to do this kind of microscopy; this is far from a solved problem. Experiments give us exquisite tools and theorists need to figure out how best to use them in order to study how strongly coupled liquid QGP emerges from well understood weakly coupled short distance physics.
So, the big question now is how this new liquid phase of matter that has been discovered in heavy ion collisions emerges from the fundamental theory. Insights can be obtained either by characterizing the properties of the liquid at its natural length scales or, via the kind of microscopy that hard probes provide, by studying it at the shortest length scales at which the strongly coupled fluid phenomena emerge. Or, the longest length scales at which a weakly coupled description in terms of individual quarks and gluons applies. Since we do not currently know down to what length scale the liquid description is valid or below what length scale the particle-by-particle description is valid, we need microscopes with varying resolution.
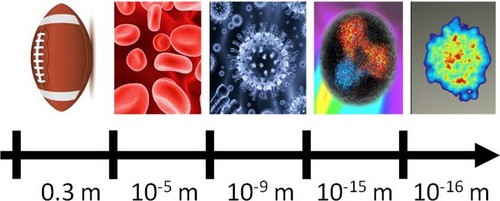
Microscopy with different resolutions. The image on the right comes from a simulation of the earliest moments of a heavy ion collision by Bjoern Schenke and collaborators. (Image Credit: NSAC Report "Implementing the 2007 Long Range Plan", January 31 2013).
You referred to the fact that we observe similar strongly coupled systems in other fields of physics and particularly in the case of cold fermionic atoms. What is so special about it?
I am not sure that we know all the ways in which the ultracold fermionic atoms, or for that matter Quark-Gluon Plasma, might be special. Both are, however, examples of liquids that flow so well, with so little dissipation, that they cannot be described just as individual quasiparticles.
One unique aspect of the ultracold atom experiments is the fact that the atomic physicists who prepare these droplets of atoms have the ability to make the coupling between individual atoms infinitely strong, in a certain sense that I could make precise. The way they do this has no analogue in QCD, but they have the advantage in their systems of a “knob” which allows them to get either an almost non-interacting gas or a strongly coupled fluid with very low shear viscosity. By setting this knob to the appropriate value, they know with confidence before they begin their experiments that they will have a system in which all the atoms in the cloud are continually interacting with all the other atoms in the cloud. There is no sense in which you can think of any atom in isolation, as If it travelled some distance before bumping into the next atom. They are all continually being jostled by all the other atoms. The fact that the atomic physicists have a tuning parameter that allows them to guarantee that their system will be in this strongly coupled regime is special to their context. Fortunately for us, it turns out that we do not need such a knob. Now, in nuclear physics we did not know before doing the experiments that we would have a strongly coupled liquid on our hands. We had to carry out the experiments, use comparisons between data and hydrodynamic calculations to constrain the shear viscosity, and then in so doing discover that QGP is a strongly coupled liquid.

A principal difference between QGP and the ultracold droplets of fermionic atoms is that QGP is relativistic while the cold atom fluid is completely non-relativistic. Hence, the two systems are certainly not identical. The cold atoms are nevertheless of interest to us because we know with confidence that they are in the strongly coupled regime. Moreover, the fact that we can take photographs of these little clouds of atoms as they explode and see the development of elliptic flow is very pleasing. It is pleasing to see the kinds of flow observables which are central to heavy ion physics arising in another strongly coupling fluid where they can literally be seen in a photograph.
Were the same patterns of behaviour expected in the nanoKelvin and the TeraKelvin scales?
I think it is fair to say that this was surprising. Certainly if you think back in time, before RHIC nobody was talking about this.
Perhaps one could rephrase the question and ask: Why is the second best liquid that we know twenty orders of magnitude colder than the best liquid that we know? QGP is literally the hottest liquid that we know and the ultracold atomic fluid is literally the coldest liquid that we know. And yet, when we characterize how well liquids flow by the appropriate dimensionless parameter that quantifies how much dissipation occurs as the liquid flows with some shear we find that these two liquids are the least dissipative liquids known. Both are described much more accurately by the laws of hydrodynamics than water is, and water is the liquid that hydrodynamics is named after!
We don’t know any reason why there could not be some room-temperature liquid that flows just as well as QGP does. There is no theoretical principle that says this cannot happen. We do not know whether the fact that the best liquids we know are the hottest and the coldest is very significant. However, the fact that the one is ultra-relativistic and the other is non-relativistic does point to an interesting story that is still being uncovered.
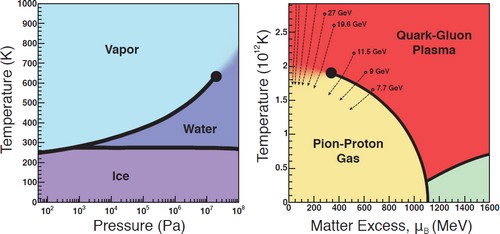
Fig. 1: (Left) Phase diagram for water. (Right) Phase diagram for quark-gluon plasma. Quark-gluon plasma made in heavy ion collisions at RHIC and the LHC energies contains almost as much antimatter as matter, and so follows the left-hand edge of the phase diagram as it cools. Lower energy collisions make quark-gluon plasma with higher excess of matter over antimatter (parameterized by the "chemical potential μB") and so can be used to explore the phase diagram. The location of the water critical point shown as a solid black circle is known and was determined by experimental measurements. The location of the critical point in the quark-gluon plasma phase diagram is unknown; it is placed where recent experiments at RHIC may be revealing hints of its presence. The green region contains superconducting forms of quark matter that may exist in the centers of neutron stars. The mapping of this phase diagram is just beginning; we know its features in the regions colored red, yellow and green but at present we have no reliable knowledge of the location of any of the boundaries between these continents (Image Credit: NSAC report, January 2013).
Theorists working on understanding the properties of QGP have built toy models for studying QGP in which it is possible to map very difficult quantum field theoretical calculations (for example like calculating the viscosity of a strongly coupled liquid) onto computationally tractable (in some cases even very easy) calculations in a gravitational theory. The strongly coupled fluid in the toy model for QCD maps onto a black hole in a curved spacetime with one higher dimension. This extra dimension encodes length scale in the quantum field theory, meaning that what we think of as studying the quantum physics of QGP via “microscopy with varying spatial resolution” maps onto studying classical physics at varying positions along this extra dimension. Many people have tried to do the same for cold atoms and although they have made much progress they have not had the same success. They have found gravitational descriptions of systems with the same nonrelativistic symmetries as the cold atom fluid, but it seems that the systems with a gravitational description that have been found so far all have equations of state that are qualitatively different from the real one.
In the case of the toy models for the Quark Gluon Plasma, the equation of state look perfectly familiar: the pressure changes with the fourth power of the temperature T, the entropy density changes with the third power of T and their coefficients have reasonable values which are similar to the ones we find in large-scale lattice calculations of QCD thermodynamics. So with the equation of state looking familiar you then go on and ask further questions like “what is the shear viscosity of the QGP?” or “how fast can QGP, flowing according to the laws of hydrodynamics, form after a collision?” and many more. In the case of cold atoms the symmetries seem to be right but the equation of state is wrong, even at the level of not having the right powers in it, so we are not sure what to make of the fact that the shear viscosity comes out reasonably well. I think there is still an opportunity for a theorist to come up with a better toy model for the cold atom fluid that would allow us to use qualitative insights gained from the gravitational description with the same confidence that we have when we use them in the QGP context.
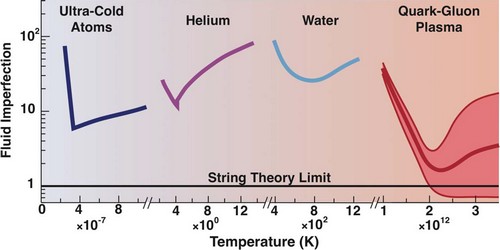
One of the exciting developments of the last few years has been the development of useful toy models that feature many phenomena that are familiar from condensed matter physics including superconductivity, “strange metals”, “non-Fermi liquids”, quantum critical points, superfluid turbulence and more. In these models, puzzling aspects of how all these phenomena work in strongly coupled many-body systems have been mapped onto tractable questions in equivalent gravitational theories. There are even examples where you can start with the gravitational description of quark-gluon plasma, crank up the excess density of some fermionic particle over that of its antiparticle, and see a strange metal emerge. This suggests that understanding quark-gluon plasma could in some way that we do not yet understand be related to understanding the non-superconducting phase of the cuprate high temperature superconductors. The phrase that is often used to describe these fast-moving developments is “many body physics through a gravitational lens”. This lens is still not completely clear, however, meaning that we have a great chance to clarify the understanding of many of these systems via developing experimental observables that can serve as microscopes with varying spatial resolution focused on “our” quark-gluon plasma.
So I would conclude by sharing my feeling that there is some new kind of universality that we are groping towards understanding. A universality which doesn’t take into account whether the fluid is relativistic or non-relativistic, and which does not much care about many microscopic details but which takes into account the degree to which the fluid is scale invariant and which only applies if the fluid is strongly coupled. I think that nobody has yet put their finger precisely on what this new type of universality is or where it applies. This is another opportunity in front of us. If there is in fact a new universality along these lines, further experimental and theoretical advances in understanding the properties of QGP will have ramifications across many other areas of science.
Which do you think will be the best probes for studying the QGP when the LHC moves to higher energies after the Long Shutdown Period?
As we have already discussed, I think there are two sides to this story. The one is about characterising the properties of quark-gluon plasma. We are learning many things from the particle spectra, ν1, v2 and higher vn’s. The new frontiers here include measuring and understanding how the correlations and event-by-event fluctuations of these quantities constrain the properties of the hydrodynamic fluid (like its viscosity) and the nature of the quantum fluctuations that were seeded in the fluid at the earliest moments of the collision. Although this story will play out in the next few years, I am not sure that I can see a way in which the new higher energies at the LHC will bring qualitatively new developments here. The advances will come from better theoretical analysis of data already in hand, from much higher statistics that will allow new correlation observables to be measured better and, at RHIC, from uranium-uranium and copper-cold collisions that vary the shape of the initial droplet of QGP.
The big advantage of higher energy collisions will be that they allow us access to higher energy hard probes of the QGP. For example, the energy of the available jets will increase. The increased collision energy should also play a great role in advancing the study of gamma-jet events by making them more numerous than in the current data set. In these events, a single hard photon is produced back-to-back with what was initially a high momentum quark. The photon flies out of the QGP without being affected by it. So, the energy and the direction of this photon tell us the initial energy and direction of the quark directly. Then, you can look at the jet that comes out and learn in a very quantitative way how its properties have been modified. How much energy did this particular high momentum quark lose as it plowed through the quark-gluon plasma? Did this high momentum quark scatter by any appreciable angle, for example if it experienced a hard scattering event off one of those weakly coupled quarks and gluons that we expect must be seen when the liquid quark-gluon plasma is imaged at high resolution? The higher collision energies coming in a few years will greatly improve the statistics of these measurements, making it possible to address these kinds of questions. I expect that we will learn a lot.
Heavy quarks and Y statistics will also improve a lot. In both cases, the proton-lead run that took place earlier this year will give us the appropriate baseline for the future 5 TeV or 5.5 TeV heavy-ion running after the shutdown. These two data sets in concert will give us precise measurements of how hard probes including Y’s and J/ψ’s and heavy quarks see the strongly coupled plasma.
I don’t expect that the basic characteristics of the plasma will change significantly compared to what we already know. In that respect, dialing up the collision energy plays quite a different role in the study of QGP than in the search for, say, supersymmetry. When searching for physics beyond the standard model, the increase in collision energy means that heavier particles can be produced for the first time. In the case of QGP, what changes in higher energy collisions is not the QGP itself but is rather the energy, and the number, of the probes of the plasma that we have access to. That’s why what I will be watching when the LHC runs at its higher energy is jet quenching, including in particular gamma-jet studies, Y's and heavy quarks which are all examples of observables where higher statistics and higher momenta can yield new insights.
I would like to focus on jet quenching and the model that you discussed in a recent TH-seminar
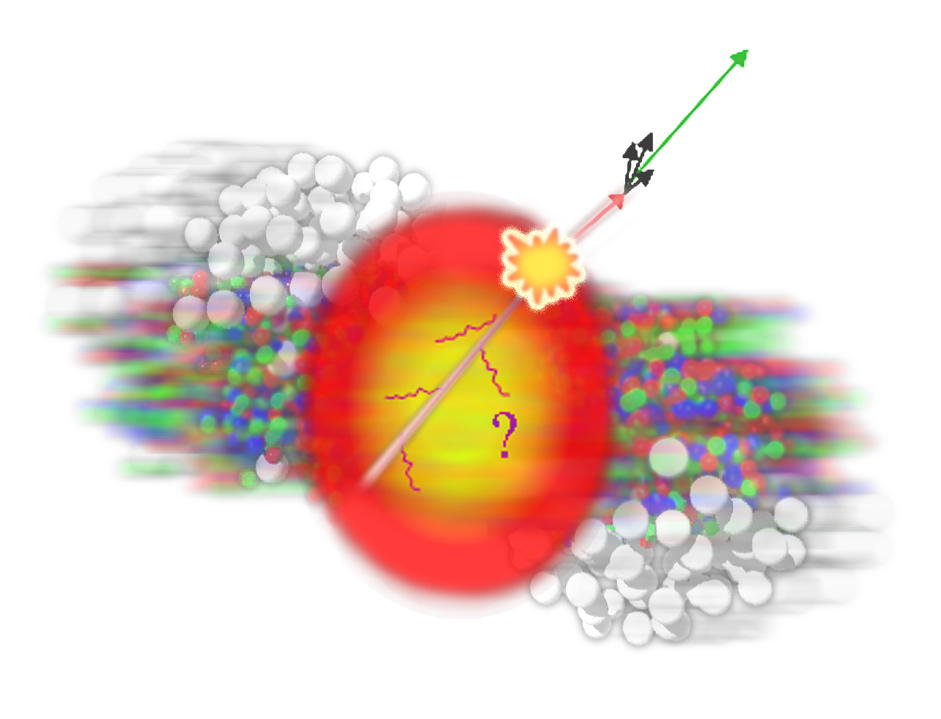
I don’t want to overstress that model. Although I think it’s very instructive it would be an overstatement to call it a model for jets, and therefore it is an overstatement to say that this model can explain jet quenching. What I described is more like a lighthouse beam than a jet. It is a tightly collimated beam of gluons that are not coherent like a laser beam. The best analogy is a lighthouse beam. Think of a beam of gluons, instead of photons, which you shine through the strongly coupled plasma. What we showed is that in these theories with an equivalent gravitational description it is possible to do reliable calculations that show how such a beam of gluons is quenched in a strongly coupled plasma and how the stopping length for such a beam changes as you change the wavelength of the gluons in the beam. I think the qualitative features we find are instructive. For example we see that the beam of gluons loses its energy without spreading in angle, very reminiscent at a qualitative level of what is seen for jets in heavy ion collisions at the LHC. The lost energy becomes sound waves which themselves quickly thermalize, which is again reminiscent of what has been seen at the LHC where the energy lost by a jet ends up as many soft particles moving in all random directions.

A quark whirling around in a small circle at ultrarelativistic speed is an artificial way to make a tightly collimated beam of gluon radiation. At one moment in time, like in these snapshots, the outward-going beam of lighthouse-like radiation is located on a spiral. In vacuum, left panel, the beam propagates outward much like a beam of synchrotron radiation does in classical electromagnetism, even though here the beam is made of strongly coupled gluons. When this beam is instead fighting its way through strongly coupled plasma, as in the right panel, it gets quenched, losing its energy to the plasma as it propagates outward.
There is a second qualitative analogy that I also find very exciting. There is some preliminary evidence from both ALICE and from experiments at RHIC that lower energy jets are associated with a broadened jet cone. So it is as if for lower energy jets at least some of the energy that is lost by the leading parton stays close to the jet cone, whereas for higher energy jets most of the lost energy ends up outside the cone, at large angles. If that is true there is a natural explanation that comes from the lighthouse beam model that I described. Lower energy jets translate into a lighthouse beam made of longer wavelength gluons that is quenched much more quickly over a shorter distance. This means that if you see any debris from such a jet at all the jet didn’t travel very far and the lost energy is in the form of sound waves moving in similar directions to the direction of the initial parton. On the other hand, a lighthouse beam with higher energy is made of shorter wavelength gluons which means that they travel farther and leave their lost energy farther behind, meaning that the lost energy has time to thermalize much more effectively. So, what comes out of these calculations are nice qualitative lessons that affect how I think of jet quenching at RHIC and the LHC.
But this is only an instructive analogy. Don’t forget that a jet is a perturbative QCD object. It’s a single virtual parton which then fragments according to the rules of perturbative QCD into a jet. So, yes, a jet is tightly collimated. But it is not a beam of classical radiation.
According to the data there are some aspects of the physics of jets in heavy ion collisions that are profoundly strongly coupled. (For example, all the properties of the medium itself, plus the fact that the energy lost by a parton that starts out with an energy of a few hundred GeV ends up in the form of very many one or two GeV hadrons going at all different angles.) However, there are also some aspects of the physics of jets in heavy ion collisions that don’t look strongly coupled at all. The fact that the hard fragments of the jet come out looking very similar to a perturbative QCD jet that is described very well by PYTHIA doesn’t sound strongly coupled at all. It seems to me that the data are telling us that some aspects of the story are weakly coupled and should be described as such while other aspects are strongly coupled and should also be described appropriately. I am currently working with several collaborators here at CERN toward developing a hybrid approach in which we look inside PYTHIA and leave the parton shower that it describes largely untouched except that we make each of the partons in the shower lose energy in the way that a single parton does in a strongly coupled plasma. It is too early to say what the outcome of this particular attempt will be but I think that the experimental data are calling for some sort of hybrid approach along these lines.
Speaking of what I am doing during my sabbatical at CERN, which has been wonderful so far, perhaps I should mention that with four coauthors (one of whom is Urs Wiedemann whom you have interviewed previously) I am currently completing a 450+ page book for Cambridge University Press in which we introduce heavy ion physics to string theorists (and others!), introduce string theory and the consequent equivalences between strongly coupled quantum field theories and classical gravitational theories with one higher dimension to heavy ion physicists (and others!), and then describe and review the many qualitative insights into strongly coupled plasma and heavy ion collisions that have been obtained by mapping hard questions onto tractable calculations in the equivalent gravitational theory. We have talked about a few of these insights. There will be many more described in the book.
Given the small size and time duration of the QGP produced in the laboratory I wonder whether it can be useful in understanding the evolution of our universe?
Learning that the stuff that filled the early Universe was a liquid doesn’t actually tell us something that could be used in order to make predictions about what we currently see with telescopes or satellites. This is precisely because astronomical observations teach us about the early universe at much longer length and time scales than are probed in heavy ion collision experiments. So, understanding the formation of QGP in the laboratory and probing its properties answers questions about the matter that filled the microseconds-old universe that will never be accessible via astronomical observations. These are complementary routes to understanding our origins.
To link that to one of your previous questions I would point to a second analogy between heavy-ion collisions and cosmology, namely the role that initial fluctuations play in the formation and evolution of the medium. In cosmology, these fluctuations may originate as quantum fluctuations in inflation while in the case of heavy-ion collisions they are quantum fluctuations originating in the fact that a nucleus is not a featureless bag of matter but is made of protons and neutrons, each having their own internal structure. In both cosmology and heavy ion collisions, however, those initial quantum fluctuations seed ripples in a fluid which evolve subsequently according to the laws of hydrodynamics. And, at the end of the day in both cases you do a multipole decomposition of the debris from the explosion. in the case of cosmology this “debris” is the cosmic microwave background radiation whose fluctuations are described by multipole coefficients called cl’s. In heavy-ion collisions the debris is the hadrons in the final state, and the multipole decomposition, parametrized by the vn’s, describes their momentum flow. From the cl’s in cosmology and the vn's in heavy ion colisions, we learn about the properties of both the fluid and the initial fluctuations. Because the cosmological observations and heavy ion collisions are sensitive to ripples in the fluid with very different wavelengths, they answer different questions about it, with only heavy ion collisions telling us about its material properties like viscosity. It is interesting that, as in cosmology, some memory of initial quantum fluctuations seems to survive to the final state and to affect v3, ν4, v5 and ν6
You can now see that there is a complementarity of a different type. In cosmology, experimentalists can measure the first few thousand cl’s because they have a very high angular resolution of the final state of their explosion. In heavy ion physics, on the other hand, we so far have measured the vn's up to n=6 and although we already have limits on the next several values of n we will never have the high angular resolution that is possible in cosmology. On the other hand, we have a big advantage since cosmologists have only one event to study while we have billions of events on tape, billions of little bangs. And, furthermore, the cosmologists must take the one big bang that nature has provided whereas we are able to tailor the initial conditions in our little bangs by colliding different nuclei and selecting collisions with different impact parameters. In addition, because we have so many events we can study event-by-event fluctuations, something that is impossible in cosmology with its single event. So the challenges are different but I think that these analogies can nevertheless be instructive.
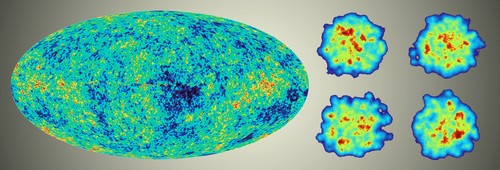
Our one universe with its primordial fluctuations (parts per million variations in temperature) as measured via photons by the WMAP satellite experiment (left) compared to seed fluctuations (corresponding to 10-15% variations in temperature) in four simulated heavy ion collisions at RHIC (right). The measured fluctuations bring us knowledge about the quantum fluctuations at the earliest moments of the explosion (big bang or heavy ion collision) as well as about the material properties of the rippling fluid that ensues. Observations of the glow of the big bang or of heavy ion collisions reveal different and complementary properties of the trillions-of-degrees-hot matter that filled the microseconds old universe (Image Credit: NSAC Report, January 2013).
Does the presence of an excess of matter over antimatter in the universe offer another possible connection between the study of QGP and cosmology?
We know that our universe has an excess of matter over antimatter. If that were not so, we would not exist! So, the question is: How did this excess originate? Physicists have been striving to answer this question for more than 40 years since the work of Andrei Sakharov in the 1960’s, who first posed it in a crisp way.
Many of the models that seek to answer this question invoke processes that occurred in the quark-gluon plasma of the early universe when it was 1000 times hotter than the plasma made in heavy ion collisions at the LHC. At these temperatures, which were last seen picoseconds after the Big Bang, the W’s and Z’s, the electroweak bosons, were both massless and copious. Although it would be wonderful to create such an electroweak plasma in the laboratory, you can see that it is impossible to do so in the foreseeable future by noticing that when we increased the collision energy by a factor of 14 in going from RHIC to the LHC the plasma temperature went up by less than a factor of 2. This makes increasing the temperature by a further factor of 1000 inconceivable. However, we are lucky because theory shows that in this electroweak plasma the dynamics of the W and Z fields are analogous to the dynamics of the gluon fields in the QCD plasma that we can study, today, in heavy ion collisions.
The processes in the electroweak plasma that turned antimatter to matter and vice versa, have precise analogues in processes that occur in the QCD plasma. In the case of the electroweak plasma these processes are called sphalerons, and they involve the W and Z fields tying themselves in knots or untying themselves. In the case of the QGP (1000 times colder but still trillions of degrees hot!) there are analogous processes in which the gluon field ties itself into knots or unties itself. When the W and Z fields in the 1000 times hotter electroweak theory tie themselves in a knot, antiquarks get converted into quarks. When they untie themselves, quarks get converted into antiquarks. If these complex dynamical processes are biased very slightly in favor of knotting versus unknotting by new physical effects that are present in many models of physics beyond the standard model, an excess of matter over antimatter results. One of the ways that physicists try to test these theories is to look for the appropriate physics beyond the standard model. It would also be very nice to have experimental confirmation that hot gauge fields really do tie themselves in knots in the way that the theory predicts. This is where heavy ion collisions that produce QGP in our labs come in.
In the QGP at temperatures that we can produce in the laboratory, when the gluon fields tie themselves up (in just the same way that the W and Z fields do at much higher temperatures) left-handed quarks get converted into right-handed quarks. When the gluon fields untie themselves, right-handed quarks get turned into left-handed quarks. In the small droplet of plasma made in a single heavy ion collision, odds are good that you’ll get more tying than untying or vice versa, not exactly the same number of each. This means that the “signature” of these kinds of complex dynamical processes in heavy ion collisions is an excess of right-handed quarks over left-handed quarks in some events, and an excess of the opposite sign in other events. So far, everything I have said has been known for decades, but nobody had proposed a way of seeing the excess of R or L quarks. The new development from the last several years has been the realization that in the presence of a large enough magnetic field an excess of R quarks results in an electric current along the direction of the magnetic field, while an excess of L quarks yields an electric current flowing against the magnetic field. Electric currents move charged particles around and can have observable effects. We have also realized that heavy ion collisions with any nonzero impact parameter feature very large magnetic fields, created by the spectator nucleons whizzing past the collision zone. The spectator nuclei create a B=1018-19 Gauss in top energy RHIC collisions, while at the LHC we get an even larger B which lasts for a shorter time. Heavy ion collisions therefore feature magnetic fields that are more than 1000 times larger than the largest astronomical magnetic fields, although these intense fields exist only in a nucleus-sized volume and only for a brief instant.
Several years ago, in a series of papers Dima Kharzeev and his colleagues put all these pieces together. They observed that if the gluon fields knot and unknot as expected, and if the expected large magnetic fields are present, and if both these conditions are met in a droplet of quark-gluon plasma in which chiral symmetry is unbroken (since the chiral symmetry breaking found at lower temperatures would mean that R quarks don’t stay R and L quarks don’t stay L, which would wash the effect out) then what should happen is that in some events positively charged particles will be pushed upwards along the magnetic field and negatively charged particles downward, and In other events vice versa. This event-by-event charge separation was estimated to be a rather small effect. Next, a signature that can be interpreted as exactly this charge separation was actually detected, first at STAR and then at ALICE.
However, it was quickly realized that this signature could also be interpreted in other, much more prosaic, ways. Without getting into details, it turns out that the prosaic interpretations of this effect require a v2. So in order to exclude these interpretations, experimentalists at RHIC tried to “turn off the QGP” by looking collisions at a very low energy that still have significant v2. If the prosaic interpretation were correct, the effect should have persisted since v2 was significant. Instead, it turned off.
They also found a way to turn off the magnetic field while keeping v2 (They did this by colliding uranium nuclei at RHIC and selecting events with no spectators, and therefore no magnetic field, that still had a significant v2 originating from the deformed shape of the incident uranium nuclei.) With this v2 present, if the prosaic interpretation were correct, the effect should again have persisted. Instead, again it turned off. Both of these results were reported at QM12 just a few months ago. There, preliminary results from a third clever experiment were also reported. The STAR collaboration selected events with an excess of positively charged particles at mid-rapidity, and saw that in such events the v2 of negatively charged particles should be greater than that of positively charged particles, just as Kharzeev and his collaborators had predicted. So, although all of these developments are very recent and will need to be scrutinized and confirmed,it is striking that the prosaic interpretations of the original STAR and ALICE have been ruled out while at least at a qualitative level the interpretation in terms of charge separation hangs together. Perhaps we are seeing the first laboratory evidence of the knotting and unknotting of gauge fields in hot plasma. Studying these phenomena in heavy ion collisions - where it is the gluon fields that are in action - can teach us about the analogous dynamics of the W and Z fields in the 1000 times hotter electroweak plasma, dynamics that may be responsible for the excess of matter over antimatter in the universe and thus for our existence. Although much remains to be done, both on the experimental side and in improving the precision of the theoretical analyses, the prospect of re-enacting and studying the mechanisms that created an excess of matter over antimatter in the very early universe is breathtaking. We shall see in a few years whether this prospect pans out; we already know that this “application” of heavy ion collisions is the only possible way to gain access to such phenomena in the laboratory.